How To Find Iqr With Mean And Standard Deviation

• Inquiry commodity
• Open Access
• Published: 19 Dec 2014

Estimating the sample mean and standard deviation from the sample size, median, range and/or interquartile range

BMC Medical Enquiry Methodology volume fourteen, Commodity number:135 (2014) Cite this article

• 122k Accesses

• 2628 Citations

• 20 Altmetric

• Metrics details

Abstract

Groundwork

In systematic reviews and meta-analysis, researchers often pool the results of the sample mean and standard departure from a set of similar clinical trials. A number of the trials, however, reported the report using the median, the minimum and maximum values, and/or the first and tertiary quartiles. Hence, in gild to combine results, one may have to gauge the sample hateful and standard deviation for such trials.

Methods

In this paper, we propose to meliorate the existing literature in several directions. Beginning, we show that the sample standard deviation estimation in Hozo et al.'s method (BMC Med Res Methodol 5:13, 2005) has some serious limitations and is always less satisfactory in do. Inspired past this, we advise a new interpretation method past incorporating the sample size. Second, we systematically study the sample mean and standard divergence interpretation problem under several other interesting settings where the interquartile range is likewise available for the trials.

Results

Nosotros demonstrate the performance of the proposed methods through simulation studies for the three often encountered scenarios, respectively. For the first two scenarios, our method greatly improves existing methods and provides a near unbiased gauge of the truthful sample standard deviation for normal data and a slightly biased estimate for skewed data. For the third scenario, our method still performs very well for both normal data and skewed data. Furthermore, nosotros compare the estimators of the sample hateful and standard deviation under all 3 scenarios and present some suggestions on which scenario is preferred in real-world applications.

Conclusions

In this newspaper, nosotros discuss different approximation methods in the estimation of the sample hateful and standard deviation and suggest some new estimation methods to improve the existing literature. Nosotros conclude our work with a summary tabular array (an Excel spread sheet including all formulas) that serves as a comprehensive guidance for performing meta-assay in different situations.

Peer Review reports

Groundwork

In medical enquiry, it is mutual to find that several similar trials are conducted to verify the clinical effectiveness of a certain treatment. While individual trial study could fail to evidence a statistically significant handling effect, systematic reviews and meta-analysis of combined results might reveal the potential benefits of treatment. For example, Antman et al. [ane] pointed out that systematic reviews and meta-analysis of randomized command trials would take led to earlier recognition of the benefits of thrombolytic therapy for myocardial infarction and may save a big number of patients.

Prior to the 1990s, the traditional arroyo to combining results from multiple trials is to comport narrative (unsystematic) reviews, which are mainly based on the experience and subjectivity of experts in the surface area [2]. However, this approach suffers from many critical flaws. The major one is due to inconsistent criteria of different reviewers. To claim a handling outcome, different reviewers may use different thresholds, which oftentimes lead to opposite conclusions from the same study. Hence, from the mid-1980s, systematic reviews and meta-analysis have become an imperative tool in medical effectiveness measurement. Systematic reviews employ specific and explicit criteria to place and assemble related studies and usually provide a quantitative (statistic) gauge of amass issue over all the included studies. The methodology in systematic reviews is usually referred to equally meta-assay. With the combination of several studies and more than data taken into consideration in systematic reviews, the accuracy of estimations will get improved and more precise interpretations towards the treatment event can be achieved via meta-assay.

In meta-analysis of continuous outcomes, the sample size, mean, and standard deviation are required from included studies. This, however, can be difficult because results from different studies are often presented in unlike and non-consistent forms. Specifically in medical inquiry, instead of reporting the sample hateful and standard deviation of the trials, some trial studies only report the median, the minimum and maximum values, and/or the first and third quartiles. Therefore, we need to estimate the sample mean and standard departure from these quantities then that we can pool results in a consistent format. Hozo et al. [three] were the first to accost this estimation problem. They proposed a unproblematic method for estimating the sample mean and the sample variance (or equivalently the sample standard deviation) from the median, range, and the size of the sample. Their method is now widely accepted in the literature of systematic reviews and meta-analysis. For instance, a search of Google Scholar on November 12, 2014 showed that the article of Hozo et al.'s method has been cited 722 times where 426 citations are made recently in 2013 and 2014.

In this newspaper, we will show that the estimation of the sample standard divergence in Hozo et al.'south method has some serious limitations. In item, their estimator did non incorporate the information of the sample size so consequently, it is always less satisfactory in practice. Inspired past this, we propose a new estimation method that will greatly meliorate their method. In addition, we will investigate the estimation trouble under several other interesting settings where the first and 3rd quartiles are as well available for the trials.

Throughout the paper, we define the following summary statistics:

a = the minimum value,

q ₁ = the commencement quartile,

1000 = the median,

q ₃ = the third quartile,

b = the maximum value,

n = the sample size.

The {a,q ₁,m,q ₃,b} is often referred to as the 5-number summary [4]. Note that the 5-number summary may non always be given in full. The three frequently encountered scenarios are:

$${\mathcal{C}}_{\mathrm{ii}}=\{a,q_{\mathrm{i}},\mathrm{thousand},q_3,b;n\},$$

Hozo et al.'southward method just addressed the interpretation of the sample mean and variance nether Scenario ${\mathcal{C}}_{\mathrm{one}}$ while Scenarios ${\mathcal{C}}_2$ and ${\mathcal{C}}_3$ are also common in systematic review and meta-analysis. In Sections 'Methods' and 'Results', we written report the interpretation problem under these three scenarios, respectively. Simulation studies are conducted in each scenario to demonstrate the superiority of the proposed methods. We conclude the paper in Section 'Word' with some discussions and a summary table to provide a comprehensive guidance for performing meta-assay in different situations.

Methods

Estimating $\overline{\mathrm{10}}$ and S from ${\mathcal{C}}_1$

Scenario ${\mathcal{C}}_{\mathrm{ane}}$ assumes that the median, the minimum, the maximum and the sample size are given for a clinical trial study. This is the same assumption as made in Hozo et al.'s method. To estimate the sample hateful and standard deviation, we outset review the Hozo et al.'south method and point out some limitations of their method in estimating the sample standard departure. We then propose to improve their estimation by incorporating the information of the sample size.

Throughout the paper, we let X ₁,X ₂,…,X _n be a random sample of size due north from the normal distribution Northward(μ,σ ²), and X _(ane)≤Ten ₍₂₎≤⋯≤10 _(n) be the ordered statistics of 10 _ane,X _two,⋯,X _north . As well for the sake of simplicity, we assume that n = 4Q + 1 with Q being a positive integer. And then

$$\begin{array}{ll}a=X_{\left(\mathrm{one}\right)}& \le X_{\left(\mathrm{two}\right)}\le \cdots \le X_{(Q+1)}=q_{\mathrm{one}}\\ \le X_{(Q+\mathrm{two})}\le \cdots \le X_{(2Q+\mathrm{ane})}=\mathrm{thousand}\\ \le X_{(2Q+2)}\le \cdots \le {\mathrm{Ten}}_{(3Q+\mathrm{i})}=q_3\\ \le X_{(3Q+2)}\le \cdots \le X_{(4Q+\mathrm{i})}=X_{\left(n\right)}=\mathrm{b.}\end{array}$$

(1)

In this section, we are interested in estimating the sample mean $\overline{\mathrm{Ten}}={\sum }_{i=\mathrm{i}}^{\mathrm{northward}}{\mathrm{Ten}}_i$ and the sample standard deviation $\mathrm{Due\; south}={\left[{\sum }_{i=1}^n{({\mathrm{10}}_i-\bar{X})}^2/(\mathrm{north}-1)\right]}^{1/\mathrm{ii}}$, given that a,m,b, and n of the data are known.

Hozo et al.'s method

For ease of note, let Yard = 2Q + 1. Then, 1000 = (n + 1)/ii. To guess the mean value, Hozo et al. applied the following inequalities:

$$\begin{array}{l}a\le X_{\left(1\right)}\le a\\ a\le X_{\left(i\right)}\le \mathrm{yard}(i=2,\dots ,M-1)\\ \mathrm{thousand}\le X_{\left(\mathrm{One\; thousand}\right)}\le m\\ \mathrm{1000}\le {\mathrm{Ten}}_{\left(i\right)}\le b(i=\mathrm{Chiliad}+\mathrm{ane},\dots ,\mathrm{northward}-\mathrm{ane})\\ b\le {\mathrm{Ten}}_{\left(\mathrm{northward}\right)}\le \mathrm{b.}\end{array}$$

Calculation up all above inequalities and dividing by n, we have ${\mathit{\text{LB}}}_{\mathrm{one}}\le \bar{X}\le {\mathit{\text{UB}}}_{\mathrm{i}}$, where the lower and upper premises are

$$\begin{array}{l}{\mathit{\text{LB}}}_1=\frac{a+m}{2}+\frac{2b-a-\mathrm{yard}}{2\mathrm{north}},\\ {\mathit{\text{UB}}}_{\mathrm{one}}=\frac{m+b}{2}+\frac{2a-m-b}{\mathrm{two}\mathrm{due\; north}}.\end{array}$$

Hozo et al. so estimated the sample mean by

$$\begin{array}{l}\frac{{\mathit{\text{LB}}}_1+{\mathit{\text{UB}}}_{\mathrm{one}}}{\mathrm{ii}}=\frac{a+2\mathrm{thousand}+b}{4}+\frac{a-2\mathrm{one\; thousand}+b}{4n}.\end{array}$$

(ii)

Annotation that the second term in (ii) is negligible when the sample size is large. A simplified mean estimation is given as

$$\begin{array}{l}\bar{X}\approx \frac{a+2\mathrm{thou}+b}{4}.\end{array}$$

(3)

For estimating the sample standard deviation, by bold that the data are non-negative, Hozo et al. applied the following inequalities:

$$\begin{array}{lll}{\mathit{\text{aX}}}_{\left(1\right)}\le & X_{\left(1\right)}^{\mathrm{two}}& \le {\mathit{\text{aX}}}_{\left(\mathrm{one}\right)}\\ {\mathit{\text{aX}}}_{\left(i\right)}\le & X_{\left(i\right)}^2& \le {\mathit{\text{mX}}}_{\left(i\right)}(i=2,\dots ,\mathrm{Yard}-\mathrm{ane})\\ {\mathit{\text{mX}}}_{\left(\mathrm{1000}\right)}\le & X_{\left(M\right)}^2& \le {\mathit{\text{mX}}}_{\left(\mathrm{Thousand}\right)}\\ {\mathit{\text{mX}}}_{\left(i\right)}\le & X_{\left(i\right)}^2& \le {\mathit{\text{bX}}}_{\left(i\right)}(i=M+1,\dots ,\mathrm{due\; north}-1)\\ {\mathit{\text{bX}}}_{\left(\mathrm{northward}\right)}\le & {\mathrm{10}}_{\left(n\right)}^2& \le {\mathit{\text{bX}}}_{\left(n\right)}.\end{array}$$

(4)

With some unproblematic algebra and approximations on the formula (4), we have ${\mathit{\text{LSB}}}_1\le {\sum }_{i=\mathrm{one}}^{\mathrm{north}}{X}_i^{\mathrm{ii}}\le {\mathit{\text{USB}}}_{\mathrm{one}}$, where the lower and upper bounds are

$$\begin{array}{l}{\mathit{\text{LSB}}}_1=a^2+{\mathrm{thousand}}^2+b^2+(M-2)\frac{a^{\mathrm{ii}}+\mathit{\text{am}}+g^{\mathrm{ii}}+\mathit{\text{mb}}}{\mathrm{ii}},\\ {\mathit{\text{USB}}}_{\mathrm{one}}=a^{\mathrm{two}}+m^{\mathrm{ii}}+b^2+(\mathrm{One\; thousand}-2)\frac{\mathit{\text{am}}+m^{\mathrm{ii}}+\mathit{\text{mb}}+b^2}{2}.\end{array}$$

Then by (iii) and the approximation ${\sum }_{i=1}^{\mathrm{north}}{X}_i^2\approx ({\mathit{\text{LSB}}}_1+{\mathit{\text{USB}}}_1)/2$, the sample standard deviation is estimated by $\mathrm{Due\; south}=\sqrt{S^2}$, where

$$\begin{array}{ll}{S}^2& =\frac{1}{\mathrm{due\; north}-1}\left(\sum _{i=\mathrm{ane}}^{\mathrm{north}}{X}_i^{\mathrm{two}}-n{\bar{X}}^{\mathrm{ii}}\right)\\ \approx \frac{\mathrm{one}}{\mathrm{northward}-1}\left(a^2+m^{\mathrm{ii}}+b^2+\frac{(n-3)}{\mathrm{two}}\frac{{(a+m)}^2+{(\mathrm{thou}+b)}^2}{\mathrm{iv}}\right.\\ -\left.\frac{\mathrm{due\; north}{(a+2\mathrm{one\; thousand}+b)}^2}{16}\right).\end{array}$$

When due north is big, it results in the following well-known range dominion of pollex:

Note that the range rule of thumb (five) is contained of the sample size. It may not work well in do, especially when n is extremely modest or large. To overcome this problem, Hozo et al. proposed the following improved range rule of pollex with respect to the different size of the sample:

$$\begin{array}{l}S\approx \left\{\begin{array}{ll}\frac{\mathrm{i}}{\sqrt{12}}{\left[{(b-a)}^2+\frac{{(a-2m+b)}^2}{4}\right]}^{1/2}& n\le 15\\ \frac{b-a}{4}& 15<n\le 70\\ \frac{b-a}{\mathrm{vi}}& \mathrm{northward}>\mathrm{seventy},\end{array}\right.\end{array}$$

(vi)

where the formula for northward ≤ fifteen is derived under the equidistantly spaced data assumption, and the formula for n > 70 is suggested by the Chebyshev'southward inequality [5]. Note also that when the data are symmetric, we have a + b ≈ 2m and so

$$\begin{array}{l}\frac{1}{\sqrt{12}}{\left[{(b-a)}^2+\frac{{(a-2m+b)}^{\mathrm{two}}}{\mathrm{four}}\right]}^{1/2}\approx \frac{b-a}{\sqrt{12}}.\end{array}$$

Hozo et al. showed that the adaptive formula (6) performs better than the original formula (5) in most settings.

Improved estimation of South

We recollect, withal, that the adaptive formula (6) may still be less authentic for practical use. Outset, the threshold values 15 and 70 are suggested somewhat arbitrarily. Second, given the normal data N(μ,σ ²) with σ > 0 being a finite value, nosotros know that σ ≈ (b - a)/6 → ∞ as n → ∞. This contradicts to the assumption that σ is a finite value. Third, the non-negative data assumption in Hozo et al.'s method is also quite restrictive.

In this section, we propose a new estimator to farther improve (6) and, in addition, we remove the non-negative assumption on the data. Allow Z ₁,…,Z _n exist independent and identically distributed (i.i.d.) random variables from the standard normal distribution N(0,1), and Z _(i)≤⋯≤Z _(n) exist the ordered statistics of Z ₁,…,Z _n . And so X _i = μ+σ Z _i and X _(i) = μ+σ Z _(i) for i = one,…,n. In particular, we take a = μ+σ Z ₍₁₎ and b = μ+σ Z _(n). Since E(Z ₍₁₎) = -Eastward(Z _(north)), nosotros take E(b - a) = iiσ Due east(Z _{(due north)}). Hence, by letting ξ(n) = iiE(Z _(northward)), we choose the following interpretation for the sample standard deviation:

Note that ξ(north) plays an important role in the sample standard difference estimation. If we allow ξ(n) ≡ 4, then (7) reduces to the original rule of thumb in (5). If nosotros let $\xi \left(\mathrm{due\; north}\right)=\sqrt{12}$ for due north ≤ 15, 4 for fifteen < n ≤ seventy, or 6 for n > lxx, and then (seven) reduces to the improved rule of thumb (6).

Adjacent, nosotros present a method to approximate ξ(due north) and found an adaptive rule of thumb for standard departure estimation. By David and Nagaraja'south method [6], the expected value of Z _{(due north)} is

$$E\left(Z_{\left(\mathrm{north}\right)}\right)=\mathrm{north}{\int }_{-\infty }^{\infty }z{\left[\Phi \right(z\left)\right]}^{\mathrm{north}-\mathrm{i}}\varphi \left(z\right)\mathit{\text{dz}},$$

where $\varphi \left(z\right)=\frac{1}{\sqrt{2\pi }}{e}^{-z^{\mathrm{ii}}/\mathrm{two}}$ is the probability density office and $\Phi \left(z\right)={\int }_{-\infty }^z\varphi \left(t\right)\mathit{\text{dt}}$ is the cumulative distribution function of the standard normal distribution. For ease of reference, we have computed the values of ξ(n) by numerical integration using the calculator in Table 1 for northward up to 50. From Table i, it is evident that the adaptive formula (6) in Hozo et al.'s method is less accurate and also less flexible.

Table 1 Values of ξ ( n ) in the formula ( seven ) and the formula ( 12 ) for n ≤ 50

Total size table

When n is large (say n > 50), we can apply Blom's method [7] to approximate E(Z _(northward)). Specifically, Blom suggested the following approximation for the expected values of the club statistics:

$$\begin{array}{l}E\left(Z_{\left(r\right)}\right)\approx {\Phi }^{-1}\left(\frac{r-\alpha }{n-2\alpha +1}\right),r=1,\dots ,n,\end{array}$$

(viii)

where Φ ^-1(z) is the inverse function of Φ(z), or equivalently, the upper zthursday percentile of the standard normal distribution. Blom observed that the value of α increases as northward increases, with the lowest value being 0.330 for n = 2. Overall, Blom suggested α = 0.375 equally a compromise value for practical utilize. Further discussion on the pick of α can exist seen, for example, in [8] and [9]. Finally, by (7) and (8) with r = n and α = 0.375, nosotros approximate the sample standard departure by

$$\begin{array}{l}S\approx \frac{b-a}{2{\Phi }^{-1}\left(\frac{n-0.375}{\mathrm{northward}+0.25}\right)}.\end{array}$$

(9)

In the statistical software R, the upper zth percentile Φ ^-one(z) tin exist computed by the control "qnorm(z)".

Estimating $\bar{X}$ and S from ${\mathcal{C}}_{\mathrm{ii}}$

Scenario ${\mathcal{C}}_{\mathrm{ii}}$ assumes that the beginning quartile, q _one, and the third quartile, q _three, are also available in improver to ${\mathcal{C}}_1$. In this setting, Bland'south method [10] extended Hozo et al.'s results by incorporating the additional information of the interquartile range (IQR). He further claimed that the new estimators for the sample mean and standard deviation are superior to those in Hozo et al.'s method. In this section, we first review the Bland's method and point out some limitations of this method. We then, accordingly, suggest to improve this method by incorporating the size of a sample.

Bland'due south method

Noting that n = 4Q + 1, we take Q = (n - i)/4. To estimate the sample mean, Bland's method considered the following inequalities:

$$\begin{array}{lll}a\le & X_{\left(\mathrm{ane}\right)}& \le a\\ a\le & {\mathrm{Ten}}_{\left(i\right)}& \le q_1(i=2,\dots ,Q)\\ q_{\mathrm{one}}\le & X_{(Q+1)}& \le q_1\\ q_{\mathrm{i}}\le & {\mathrm{10}}_{\left(i\right)}& \le \mathrm{one\; thousand}(i=Q+2,\dots ,2Q)\\ m\le & X_{(2Q+1)}& \le \mathrm{thou}\\ \mathrm{chiliad}\le & X_{\left(i\right)}& \le q_{\mathrm{three}}(i=2Q+2,\dots ,3Q)\\ q_{\mathrm{three}}\le & X_{(3Q+1)}& \le q_3\\ q_3\le & X_{\left(i\right)}& \le b(i=3Q+\mathrm{two},\dots ,n-\mathrm{i})\\ b\le & {\mathrm{10}}_{\left(n\right)}& \le \mathrm{b.}\end{array}$$

Adding upwards all above inequalities and dividing past n, it results in ${\mathit{\text{LB}}}_{\mathrm{two}}\le \overline{\mathrm{10}}\le {\mathit{\text{UB}}}_2$, where the lower and upper bounds are

$$\begin{array}{l}{\mathit{\text{LB}}}_2=\frac{a+q_{\mathrm{ane}}+k+q_{\mathrm{iii}}}{4}+\frac{4b-a-q_1-\mathrm{thousand}-q_3}{4n},\\ {\mathit{\text{UB}}}_2=\frac{q_{\mathrm{i}}+\mathrm{chiliad}+q_{\mathrm{three}}+b}{\mathrm{iv}}+\frac{4a-q_{\mathrm{one}}-m-q_3-b}{4n}.\end{array}$$

Banal so estimated the sample mean by (LB ₂ + UB ₂)/2. When the sample size is big, by ignoring the negligible second terms in LB ₂ and UB _ii, a simplified hateful estimation is given equally

$$\begin{array}{l}\bar{X}\approx \frac{a+2q_{\mathrm{one}}+2m+2q_{\mathrm{iii}}+b}{8}.\end{array}$$

(ten)

For the sample standard difference, Bland considered some similar inequalities as in (4). Then with some uncomplicated algebra and approximation, it results in ${\mathit{\text{LSB}}}_{\mathrm{two}}\le {\sum }_{i=\mathrm{ane}}^n{X}_i^2\le {\mathit{\text{USB}}}_{\mathrm{ii}}$, where the lower and upper bounds are

$$\begin{array}{ll}{\mathit{\text{LSB}}}_2& =\frac{1}{\mathrm{eight}}\left[(\mathrm{north}+3)\left(a^2+q_{\mathrm{ane}}^2+m^2+q_3^2\right)+8b^{\mathrm{two}}\right]\\ +\left.(n-\mathrm{five})({\mathit{\text{aq}}}_1+q_1\mathrm{chiliad}+{\mathit{\text{mq}}}_3+q_{3}b)\right],\\ {\mathit{\text{USB}}}_{\mathrm{ii}}& =\frac{1}{\mathrm{eight}}\left[8a^2+(n+\mathrm{three})\left(q_{\mathrm{one}}^{\mathrm{two}}+g^2+q_3^{\mathrm{two}}+b^{\mathrm{ii}}\right)\right]\\ +\left.(n-5)({\mathit{\text{aq}}}_{\mathrm{one}}+q_{1}m+{\mathit{\text{mq}}}_3+q_{3}b)\right].\end{array}$$

Next, by the approximation ${\sum }_{i=1}^{\mathrm{due\; north}}{X}_i^{\mathrm{two}}\approx ({\mathit{\text{LSB}}}_2+{\mathit{\text{USB}}}_2)/\mathrm{two}$,

$$\begin{array}{ll}{\mathrm{Due\; south}}^2\approx & \frac{\mathrm{i}}{16}\left(a^{\mathrm{two}}+\mathrm{ii}{q}_{\mathrm{ane}}^{\mathrm{ii}}+2m^{\mathrm{two}}+\mathrm{two}{q}_3^2+b^2\right)\\ +\frac{1}{8}({\mathit{\text{aq}}}_{\mathrm{one}}+q_{\mathrm{i}}\mathrm{yard}+{\mathit{\text{mq}}}_3+q_{3}b)-\frac{1}{64}(a+\mathrm{ii}{q}_1+\mathrm{two}m\\ +\mathrm{ii}{q}_3+b{)}^2.\end{array}$$

(11)

Bland's method then took the square root $\sqrt{S^2}$ to estimate the sample standard deviation. Note that the computer (11) is contained of the sample size n. Hence, it may not exist sufficient for general utilise, especially when n is small or big. In the next section, we propose an improved estimation for the sample standard deviation by incorporating the boosted information of the sample size.

Improved interpretation of S

Call back that the range b-a was used to estimate the sample standard deviation in Scenario ${\mathcal{C}}_{\mathrm{one}}$. Now for Scenario ${\mathcal{C}}_{\mathrm{two}}$, since the IQR q ₃-q _i is also known, another approach is to estimate the sample standard deviation by (q ₃-q ₁)/η(n), where η(north) is a function of due north. Taking both methods into account, we propose the following combined estimator for the sample standard deviation:

$$\begin{array}{l}S\approx \frac{\mathrm{one}}{2}\left(\frac{b-a}{\xi \left(n\right)}+\frac{q_3-q_1}{\eta \left(n\right)}\right).\end{array}$$

(12)

Post-obit Section 'Improved estimation of S', we take ξ(n) = 2E(Z _{(due north)}). Now we wait for an expression for η(northward) so that (q ₃ - q ₁)/η(north) as well provides a good estimate of Due south. By (1), we have q _ane = μ + σ Z _(Q+1) and q ₃ = μ + σ Z _(3Q+1). Then, q ₃ - q ₁ = σ(Z _(iiiQ+1) - Z _(Q+1)). Further, by noting that E(Z _(Q+one)) = -East(Z _(3Q+i)), we take Due east(q ₃ - q ₁) = iiσ E(Z _(3Q+1)). This suggests that

$$\begin{array}{l}\eta \left(\mathrm{northward}\right)=2E\left(Z_{(3Q+1)}\right).\end{array}$$

In what follows, we propose a method to compute the value of η(n). By [6], the expected value of Z _(threeQ+1) is

$$E\left(Z_{(3Q+\mathrm{i})}\right)=\frac{(4Q+\mathrm{i})!}{\left(Q\right)!\left(3Q\right)!}{\int }_{-\infty }^{\infty }z{\left[\Phi \right(z\left)\right]}^{3Q}{[1-\Phi (z\left)\right]}^Q\varphi \left(z\right)\mathrm{dz.}$$

In Table 2, we provide the numerical values of η(n) = twoEast(Z _(3Q+1)) for Q ≤ fifty using the statistical software R. When n is big, we suggest to use the formula (8) to approximate η(north). Specifically, noting that Q = (north - 1)/4, we take η(n) ≈ 2Φ ^-ane((0.75n - 0.125)/(n + 0.25)) for r = iiiQ + 1 with α = 0.375. Then consequently, for the scenario ${\mathcal{C}}_2$ we estimate the sample standard deviation by

$$\begin{array}{l}S\approx \frac{b-a}{\mathrm{four}{\Phi }^{-\mathrm{ane}}\left(\frac{n-0.375}{n+0.25}\right)}+\frac{q_3-q_1}{4{\Phi }^{-\mathrm{i}}\left(\frac{0.75n-0.125}{n+0.25}\right)}.\end{array}$$

(13)

Table 2 Values of η ( n ) in the formula ( 12 ) and the formula ( xv ) for Q ≤l, where northward =four Q +1

Total size table

We annotation that the formula (xiii) is more concise than the formula (11). The numerical comparison between the ii formulas will be given in the section of simulation study.

Estimating $\bar{X}$ and S from ${\mathcal{C}}_3$

Scenario ${\mathcal{C}}_{\mathrm{three}}$ is an alternative manner to report the study other than Scenarios ${\mathcal{C}}_{\mathrm{i}}$ and ${\mathcal{C}}_2$. It reports the first and 3rd quartiles instead of the minimum and maximum values. I main reason to report ${\mathcal{C}}_3$ is because the IQR is usually less sensitive to outliers compared to the range. For the new scenario, we notation that Hozo et al.'s method and Bland's method will no longer exist applicable. Specially, if their ideas are followed, we take the post-obit inequalities:

$$\begin{array}{lll}-\infty \le & X_{\left(i\right)}& \le q_{\mathrm{i}}(i=\mathrm{ane},\dots ,Q)\\ q_1\le & {\mathrm{Ten}}_{(Q+1)}& \le q_1\\ q_1\le & X_{\left(i\right)}& \le \mathrm{chiliad}(i=Q+2,\dots ,\mathrm{ii}Q)\\ m\le & {\mathrm{Ten}}_{(2Q+1)}& \le \mathrm{1000}\\ \mathrm{one\; thousand}\le & X_{\left(i\right)}& \le q_3(i=2Q+2,\dots ,\mathrm{iii}Q)\\ q_3\le & X_{(\mathrm{iii}Q+1)}& \le q_3\\ q_{\mathrm{iii}}\le & X_{\left(i\right)}& \le \infty ,(i=3Q+2,\dots ,\mathrm{north})\end{array}$$

where the first Q inequalities are unbounded for the lower limit, and the final Q inequalities are unbounded for the upper limit. At present calculation up all above inequalities and dividing by north, we accept $-\infty \le \overline{\mathrm{10}}\le \infty$. This shows that the approaches based on the inequalities practice not apply to Scenario ${\mathcal{C}}_{\mathrm{iii}}$.

In contrast, the following procedure is commonly adopted in the recent literature including [eleven, 12]: "If the written report provided medians and IQR, we imputed the means and standard deviations as described by Hozo et al. [[3]]. Nosotros calculated the lower and upper ends of the range by multiplying the difference between the median and upper and lower ends of the IQR by ii and adding or subtracting the product from the median, respectively". This procedure, all the same, performs very poorly in our simulations (non shown).

A quantile method for estimating $\overline{\mathrm{Ten}}$ and S

In this department, we suggest a quantile method for estimating the sample mean and the sample standard departure, respectively. In detail, nosotros outset revisit the estimation method in Scenario ${\mathcal{C}}_2$. By (10), nosotros have

$$\begin{array}{l}\bar{X}\approx \frac{a+\mathrm{two}{q}_1+2\mathrm{one\; thousand}+\mathrm{ii}{q}_3+b}{8}=\frac{a+b}{8}+\frac{q_1+m+q_{\mathrm{iii}}}{\mathrm{four}}.\end{array}$$

Now for Scenario ${\mathcal{C}}_3$, a and b are non given. Hence, a reasonable solution is to remove a and b from the estimation and keep the 2nd term. By doing so, we have the interpretation course equally $\bar{X}\approx (q_{\mathrm{one}}+\mathrm{grand}+q_{\mathrm{three}})/C$, where C is a abiding. Finally, noting that E(q ₁ + m + q _three) = iiiμ + σ E(Z _(Q+i) + Z _2Q+ane + Z _(3Q+ane)) = 3μ, nosotros let C = three and define the estimator of the sample mean as follows:

$$\begin{array}{l}\bar{X}\approx \frac{q_{\mathrm{i}}+\mathrm{thou}+q_3}{3}.\end{array}$$

(fourteen)

For the sample standard deviation, post-obit the idea in constructing (12) we suggest the post-obit estimation:

$$\begin{array}{l}S\approx \frac{q_3-q_1}{\eta \left(\mathrm{due\; north}\right)},\end{array}$$

(15)

where η(n) = 2East(Z _(3Q+ane)). As mentioned above that Due east(q ₃ - q ₁) = 2σ E(Z _(3Q+1)) = σ η(n), therefore, the reckoner (15) provides a good estimate for the sample standard deviation. The numerical values of η(n) are given in Tabular array 2 for Q ≤ 50. When north is big, by the approximation Eastward(Z _(3Q+one)) ≈ Φ ^-1((0.75northward - 0.125)/(north + 0.25)), we tin can also estimate the sample standard departure by

$$\begin{array}{l}S\approx \frac{q_{\mathrm{three}}-q_1}{2{\Phi }^{-1}\left(\frac{0.75\mathrm{north}-0.125}{n+0.25}\right)}.\end{array}$$

(16)

A similar reckoner for estimating the standard difference from IQR is provided in the Cochrane Handbook [xiii], which is defined every bit

$$\begin{array}{l}S\approx \frac{q_{\mathrm{three}}-q_1}{1.35}.\end{array}$$

(17)

Notation that the reckoner (17) is likewise independent of the sample size n and thus may not exist sufficient for full general use. As nosotros tin see from Tabular array 2, the value of η(northward) in the formula (15) converges to most 1.35 when n is big. Notation also that the denominator in formula (16) converges to 2∗ Φ ^-ane(0.75) which is 1.34898 as n tends to infinity. When the sample size is small, our method will provide more accurate estimates than the formula (17) for the standard difference estimation.

Results

Simulation study for ${\mathcal{C}}_{\mathrm{ane}}$

In this section, we conduct simulation studies to compare the performance of Hozo et al.'s method and our new method for estimating the sample standard deviation. Post-obit Hozo et al.'s settings, we consider five different distributions: the normal distribution with hateful μ = 50 and standard deviation σ = 17, the log-normal distribution with location parameter μ = four and scale parameter σ = 0.3, the beta distribution with shape parameters α = 9 and β = 4, the exponential distribution with rate parameter λ = 10, and the Weibull distribution with shape parameter k = 2 and scale parameter λ = 35. The graph of each of these distributions with the specified parameters is provided in Boosted file i. In each simulation, nosotros first randomly sample nobservations and compute the true sample standard deviation using the whole sample. We then utilize the median, the minimum and maximum values of the sample to approximate the sample standard departure past the formulas (6) and (9), respectively. To appraise the accurateness of the ii estimates, we ascertain the relative fault of each method as

$$\begin{array}{l}\mathit{\text{relative error of South}}=\frac{\mathit{\text{the estimated S}}-\mathit{\text{the truthful South}}}{\mathit{\text{the truthful Southward}}}.\end{array}$$

(18)

With 1000 simulations, we written report the average relative errors in Figure 1 for the normal distribution with the sample size ranging from 5 to 1001, and in Figure ii for the iv non-normal distributions with the sample size ranging from v to 101. For normal data which are near commonly assumed in meta-analysis, our new method provides a nearly unbiased estimate of the true sample standard deviation. Whereas for Hozo et al.'southward method, nosotros exercise observe that the best cutoff value is about n = xv for switching between the estimates $(b-a)/\sqrt{12}$ and (b - a)/4, and is about n = 70 for switching between (b - a)/four and (b - a)/half-dozen. However, its overall performance is not satisfactory by noting that the gauge always fluctuates from -xx% to 20% of the true sample standard deviation. In addition, we note that ξ(27)≈4 from Tabular array 1 and ξ(n)≈6 when Φ ^-1((n - 0.375)/(n + 0.25)) = three, that is, n = (0.375 + 0.25 ∗ Φ(iii))/(1 - Φ(3)) ≈ 463. This coincides with the simulation results in Figure 1 where the method (b - a)/4 crosses the 10-axis between n = 20 and n = xxx, and the method (b - a)/vi crosses the x-axis between n = 400 and n = 500.

Figure 1

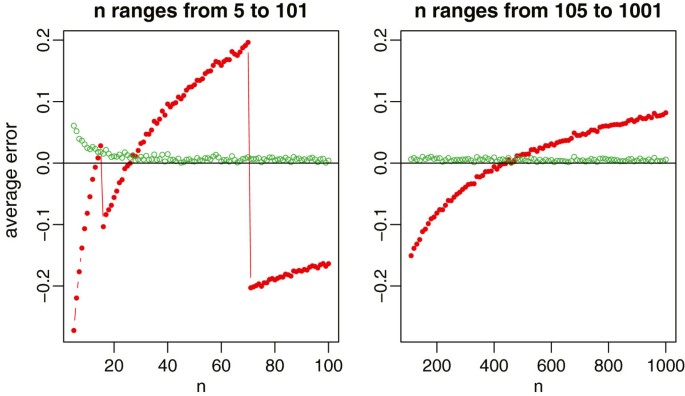
Relative errors of the sample standard deviation estimation for normal information, where the red lines with solid circles represent Hozo et al.'s method, and the green lines with empty circles stand for the new method.

Full size image

Effigy ii

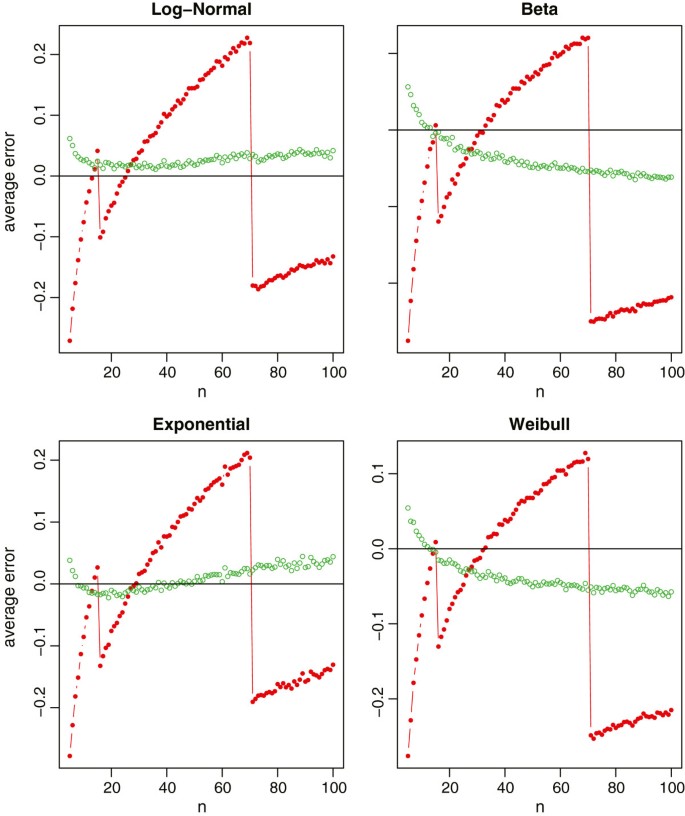
Relative errors of the sample standard difference estimation for non-normal data (log-normal, beta, exponential and Weibull), where the carmine lines with solid circles correspond Hozo et al.'due south method, and the green lines with empty circles represent the new method.

Full size epitome

From Figure 2 with the skewed data, our proposed method (9) makes a slightly biased judge with the relative errors nigh 5% of the true sample standard deviation. Nevertheless, it is still obvious that the new method is much better compared to Hozo et al.'s method. We also note that, for the beta and Weibull distributions, the best cutoff values of n should be larger than lxx for switching betwixt (b-a)/four and (b-a)/6. This again coincides with Tabular array ane in Hozo et al. [iii] where the suggested cutoff value is n = 100 for Beta and n = 110 for Weibull.

Simulation written report for ${\mathcal{C}}_2$

In this section, nosotros evaluate the performance of the proposed method (13) and compare information technology to Banal'due south method (xi). Post-obit Bland'southward settings, nosotros consider (i) the normal distribution with hateful μ = 5 and standard departure σ = i, and (ii) the log-normal distribution with location parameter μ = five and calibration parameter σ = 0.25, 0.5, and 1, respectively. For simplicity, nosotros consider the sample size being due north = Q + 1, where Q takes values from 1 to 50. As in Department 'Simulation study for ${\mathcal{C}}_{\mathrm{ane}}$

', we assess the accuracy of the two estimates by the relative mistake defined in (18).

In each simulation, we draw a full of n observations randomly from the given distribution and compute the true sample standard deviation of the sample. We then use and just utilise the minimum value, the outset quartile, the median, the third quartile, and the maximum value to approximate the sample standard divergence past the formulas (xi) and (13), respectively. With one thousand simulations, we report the average relative errors in Effigy iii for the 4 specified distributions. From Figure 3, we observe that the new method provides a nigh unbiased gauge of the true sample standard deviation. Even for the very highly skewed log-normal data with σ=1, the relative mistake of the new method is also less than ten% for most sample sizes. On the contrary, Banal's method is less satisfactory. Every bit reported in [10], the formula (11) just works for a small range of sample sizes (In our simulations, the range is nearly from 20 to 40). When the sample size gets larger or the distribution is highly skewed, the sample standard deviations volition be highly overestimated. Additionally, we note that the sample standard deviations will be seriously underestimated if n is very pocket-sized. Overall, it is axiomatic that the new method is meliorate than Bland's method in virtually settings.

Effigy iii

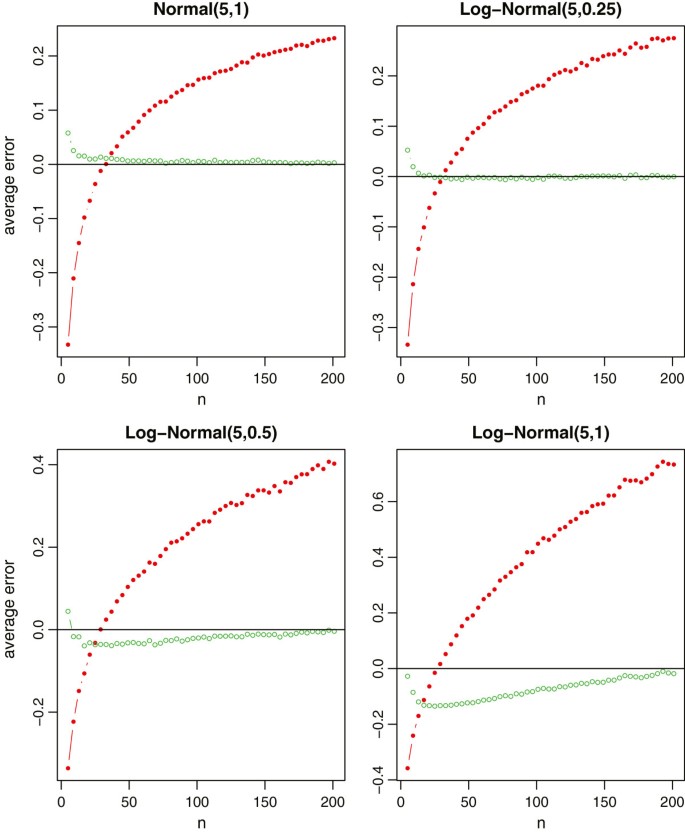
Relative errors of the sample standard deviation estimation for normal data and log-normal data, where the red lines with solid circles correspond Bland'south method, and the light-green lines with empty circles correspond the new method.

Full size epitome

Simulation study for ${\mathcal{C}}_{\mathrm{three}}$

In the third simulation study, nosotros comport a comparison report that not but assesses the accuracy of the proposed method under Scenario ${\mathcal{C}}_3$, but also addresses a more than realistic question in meta-analysis, "For a clinical trial written report, which summary statistics should be preferred to report, ${\mathcal{C}}_1$, ${\mathcal{C}}_2$ or ${\mathcal{C}}_3$ ? and why?"

For the sample mean estimation, we consider the formulas (3), (ten), and (14) under three different scenarios, respectively. The accuracy of the mean estimation is as well assessed by the relative error, which is defined in the same way as that for the sample standard deviation estimation. Similarly, for the sample standard difference estimation, nosotros consider the formulas (nine), (13), and (15) under 3 different scenarios, respectively. The distributions we considered are the same as in Section 'Simulation report for ${\mathcal{C}}_{\mathrm{ane}}$

', i.e., the normal, log-normal, beta, exponential and Weibull distributions with the aforementioned parameters as those in previous ii simulation studies.

In each simulation, nosotros first draw a random sample of size n from each distribution. The true sample mean and the truthful sample standard deviation are computed using the whole sample. The summary statistics are as well computed and categorized into Scenarios ${\mathcal{C}}_{\mathrm{one}}$, ${\mathcal{C}}_2$ and ${\mathcal{C}}_3$. We then use the aforementioned formulas to estimate the sample mean and standard divergence, respectively. The sample sizes are n = fourQ + 1, where Q takes values from ane to 50. With 1000 simulations, we report the average relative errors in Figure iv for both $\bar{X}$ and S with the normal distribution, in Effigy 5 for the sample mean interpretation with the not-normal distributions, and in Figure 6 for the sample standard deviation estimation with the non-normal distributions.

Figure 4

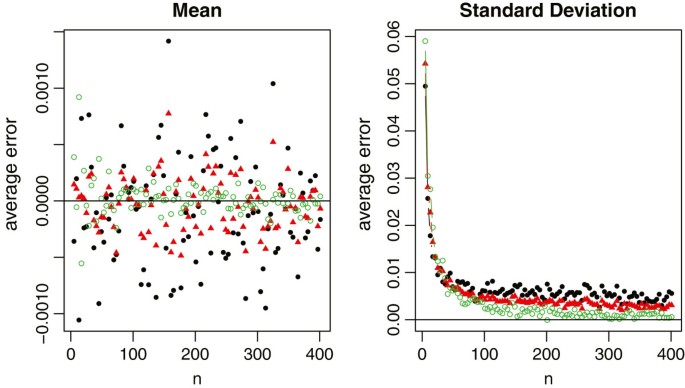
Relative errors of the sample mean and standard deviation estimations for normal data, where the black solid circles represent the method nether scenario ${\mathcal{C}}_1$ , the red solid triangles represent the method under scenario ${\mathcal{C}}_{\mathrm{two}}$ , and the dark-green empty circles represent the method under scenario ${\mathcal{C}}_3$ .

Full size image

Figure 5

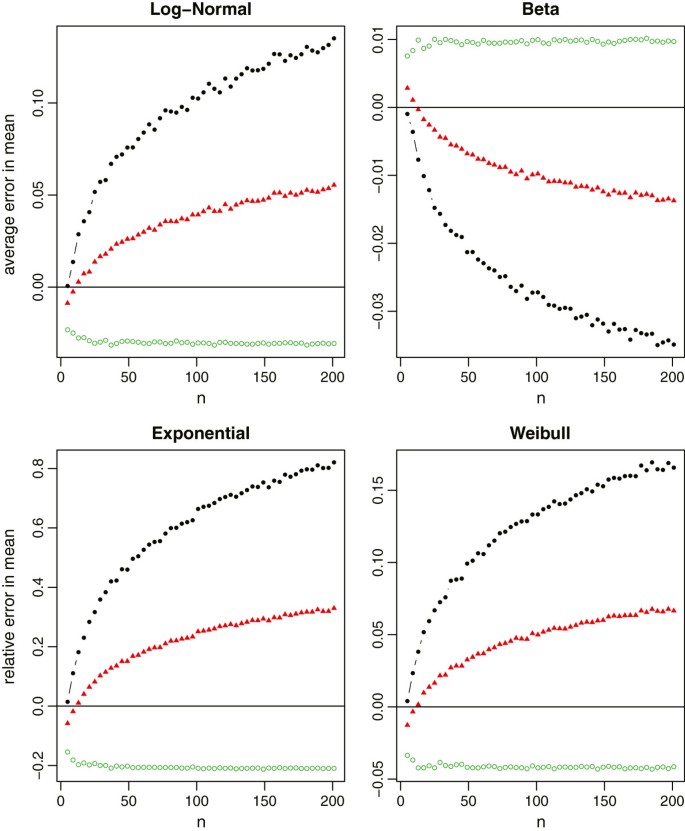
Relative errors of the sample mean interpretation for non-normal data (log-normal, beta, exponential and Weibull), where the blackness lines with solid circles represent the method under scenario ${\mathcal{C}}_{\mathrm{ane}}$ , the red lines with solid triangles represent the method under scenario ${\mathcal{C}}_{\mathrm{two}}$ , and the green lines with empty circles represent the method under scenario ${\mathcal{C}}_3$ .

Full size image

Figure 6

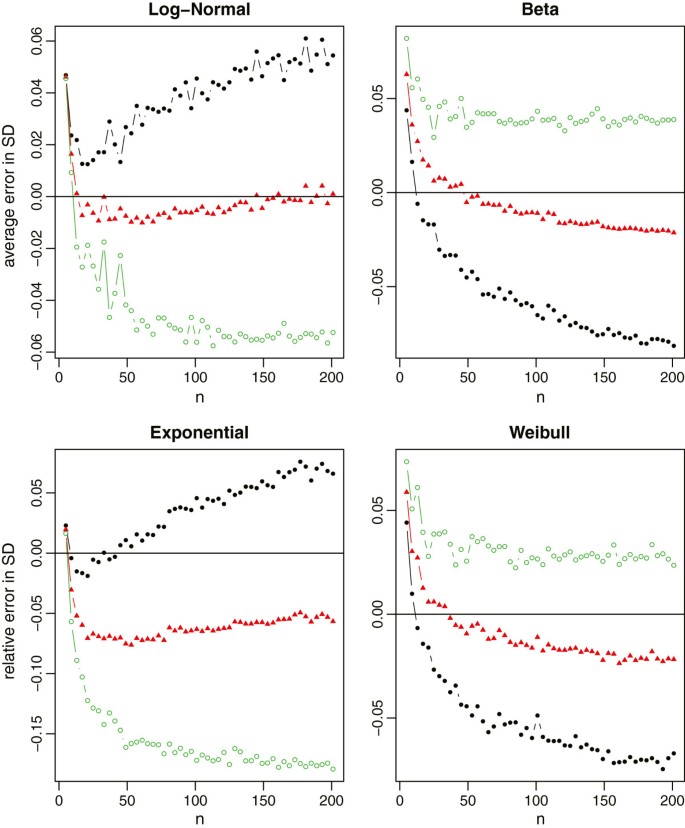
Relative errors of the sample standard deviation interpretation for non-normal data (log-normal, beta, exponential and Weibull), where the blackness lines with solid circles represent the method under scenario ${\mathcal{C}}_1$ , the red lines with solid triangles represent the method under scenario ${\mathcal{C}}_2$ , and the green lines with empty circles stand for the method under scenario ${\mathcal{C}}_3$ .

Full size paradigm

For normal data which meta-analysis would commonly assume, all 3 methods provide a most unbiased estimate of the truthful sample mean. The relative errors in the sample standard divergence estimation are also very modest in most settings (inside 1% in general). Among the three methods, however, we recommend to estimate $\bar{X}$ and Due south using the summary statistics in Scenario ${\mathcal{C}}_3$. One main reason is considering the first and 3rd quartiles are usually less sensitive to outliers compared to the minimum and maximum values. Consequently, ${\mathcal{C}}_{\mathrm{three}}$ produces a more stable interpretation than ${\mathcal{C}}_{\mathrm{i}}$, and also ${\mathcal{C}}_{\mathrm{two}}$ that is partially affected by the minimum and maximum values.

For non-normal data from Effigy 5, we note that the mean estimation from ${\mathcal{C}}_2$ is always meliorate than that from ${\mathcal{C}}_1$. That is, if the additional data in the first and third quartiles is available, nosotros should always use such information. On the other hand, the estimation from ${\mathcal{C}}_2$ may not be consistently better than that from ${\mathcal{C}}_3$ fifty-fifty though ${\mathcal{C}}_2$ contains the additional information of minimum and maximum values. The reason is that this additional information may contain extreme values which may not be fully reliable and thus atomic number 82 to worse estimation. Therefore, we need to be cautious when making the selection between ${\mathcal{C}}_{\mathrm{two}}$ and ${\mathcal{C}}_{\mathrm{iii}}$. It is too noteworthy that (i) the mean estimation from ${\mathcal{C}}_{\mathrm{three}}$ is not sensitive to the sample size, and (2) ${\mathcal{C}}_1$ and ${\mathcal{C}}_3$ always pb to reverse estimations (1 underestimates and the other overestimates the true value). While from Figure half dozen, we discover that (i) the standard deviation estimation from ${\mathcal{C}}_3$ is quite sensitive to the skewness of the data, (ii) ${\mathcal{C}}_1$ and ${\mathcal{C}}_3$ would also lead to the contrary estimations except for very small sample sizes, and (iii) ${\mathcal{C}}_2$ turns out to be a good compromise for estimating the sample standard deviation. Taking both into account, we recommend to report Scenario ${\mathcal{C}}_2$ in clinical trial studies. However, if nosotros do non have all data in the 5-number summary and have to make a decision between ${\mathcal{C}}_1$ and ${\mathcal{C}}_3$, we recommend ${\mathcal{C}}_{\mathrm{i}}$ for modest sample sizes (say northward ≤ 30), and ${\mathcal{C}}_{\mathrm{three}}$ for large sample sizes.

Discussion

Researchers ofttimes use the sample mean and standard difference to perform meta-analysis from clinical trials. Yet, sometimes, the reported results may but include the sample size, median, range and/or IQR. To combine these results in meta-analysis, we need to estimate the sample mean and standard departure from them. In this newspaper, nosotros offset show the limitations of the existing works then propose some new estimation methods. Here we summarize all discussed and proposed estimators under unlike scenarios in Table three.

Table 3 Summary table for estimating $\bar{X}$ and S nether unlike scenarios

Full size table

We note that the proposed methods are established under the supposition that the information are normally distributed. In meta-analysis, however, the medians and quartiles are ofttimes reported when data practise not follow a normal distribution. A natural question arises: "To which extent it makes sense to employ methods that are based on a normal distribution assumption?" In practise, if the entire sample or a large part of the sample is known, standard methods in statistics can be applied to guess the skewness or even the density of the population. For the current written report, however, the information provided is very express, say for example, only a, m, b and n are given in Scenario 1. Under such situations, it may non be feasible to obtain a reliable approximate for the skewness unless we specify the underlying distribution for the population. Annotation that the underlying distribution is unlikely to be known in practice. Instead, if we arbitrarily choose a distribution (more than likely to be misspecified), and then the estimates from the incorrect model can be fifty-fifty worse than that from the normal distribution assumption. As a compromise, we look that the proposed formulas under the normal distribution assumption are amidst the best we can achieve.

Secondly, nosotros note that even if the means and standard deviations can be satisfyingly estimated from the proposed formulas, it however remains a question to which extent it makes sense to use them in a meta-analysis, if the underlying distribution is very disproportionate and one must presume that they don't represent location and dispersion adequately. Overall, this is a very practical nevertheless challenging question and may warrant more than enquiry. In our future enquiry, we advise to develop some examination statistics (likelihood ratio test, score exam, etc) for pre-testing the hypothesis that the distribution is symmetric (or normal) under the scenarios we considered in this article. The result of the pre-test will so suggest the states whether or not we should nonetheless include the (very) asymmetric data in the meta-analysis. Other proposals that address this issue volition too be considered in our future written report.

Finally, to promote the usability, we have provided an Excel spread sail to include all formulas in Tabular array 3 in Boosted file 2. Specifically, in the Excel spread sheet, our proposed methods for estimating the sample mean and standard difference can be applied by simply inputting the sample size, the median, the minimum and maximum values, and/or the kickoff and third quartiles for the appropriate scenario. Furthermore, for ease of comparison, nosotros accept also included Hozo et al.'southward method and Bland's method in the Excel spread sheet.

Conclusions

In this newspaper, we discuss different approximation methods in the interpretation of the sample mean and standard deviation and propose some new estimation methods to improve the existing literature. Through simulation studies, we demonstrate that the proposed methods profoundly meliorate the existing methods and enrich the literature. Specifically, we betoken out that the widely accepted calculator of standard deviation proposed by Hozo et al. has some serious limitations and is always less satisfactory in practise because the figurer does not fully incorporate the sample size. Every bit we explained in Section 'Estimating $\bar{X}$ and South from ${\mathcal{C}}_1$ ', using (b - a)/vi for n > 70 in Hozo et al.'due south adaptive estimation is untenable because the range b - a tends to be infinity as n approaches infinity if the distribution is not bounded, such equally the normal and log-normal distributions. Our estimator replaces the adaptively selected thresholds ($\sqrt{12},4,6)$ with a unified quantity 2Φ ^-one((due north - 0.375)/(n + 0.25)), which can exist quickly computed and apparently is more than stable and adaptive. In improver, our method removes the not-negative data assumption in Hozo et al.'due south method and and then is more applicable in practise.

Bland's method extended Hozo et al.'due south method by using the boosted information in the IQR. Since extra information is included, it is expected that Bland'southward estimators are superior to those in Hozo et al.'s method. However, the sample size is still not considered in Bland'southward method for the sample standard difference, which once again limits its capability in real-world cases. Our simulation studies show that Bland's reckoner significantly overestimates the sample standard departure when the sample size is large while seriously underestimating it when the sample size is pocket-sized. Again, we incorporate the information of the sample size in the interpretation of standard departure via ii unified quantities, 4Φ ^-1((n - 0.375)/(north + 0.25)) and 4Φ ^-ane((0.75n - 0.125)/(north + 0.25)). With some actress simply lilliputian computing costs, our method makes significant improvement over Bland'southward method when the IQR is available.

Moreover, we pay special attention to an overlooked scenario where the minimum and maximum values are not available. Nosotros bear witness that the methodology following the ideas in Hozo et al.'s method and Bland'south method volition lead to unbounded estimators and is not feasible. On the contrary, we extend the ideas of our proposed methods in the other two scenarios and again construct a unproblematic just still valid estimator. After that, we take a step forwards to compare the estimators of the sample hateful and standard deviation under all three scenarios. For simplicity, we take only considered three most usually used scenarios, including ${\mathcal{C}}_1$, ${\mathcal{C}}_2$ and ${\mathcal{C}}_{\mathrm{iii}}$, in the electric current commodity. Our method, however, can be readily generalized to other scenarios, e.g., when only {a,q ₁,q ₃,b;north} are known or when additional quantile information is given.

References

1. Antman EM, Lau J, Kupelnick B, Mosteller F, Chalmers TC: A comparison of results of meta-analyses of randomized command trials and recommendations of clinical experts: treatments for myocardial infarction. J Am Med Assoc. 1992, 268: 240-248. 10.1001/jama.1992.03490020088036.

   CAS  Commodity  Google Scholar

2. Cipriani A, Geddes J: Comparison of systematic and narrative reviews: the example of the atypical antipsychotics. Epidemiol Psichiatr Soc. 2003, 12: 146-153. ten.1017/S1121189X00002918.

   Article  PubMed  Google Scholar

3. Hozo SP, Djulbegovic B, Hozo I: Estimating the hateful and variance from the median, range, and the size of a sample. BMC Med Res Methodol. 2005, 5: 13-x.1186/1471-2288-5-xiii.

   Article  PubMed  PubMed Central  Google Scholar

4. Triola M. F: Unproblematic Statistics, 11th Ed. 2009, Addison Wesley

   Google Scholar

5. Hogg RV, Craig AT: Introduction to Mathematical Statistics. 1995, Maxwell: Macmillan Canada,

   Google Scholar

6. David HA, Nagaraja HN: Club Statistics, 3rd Ed. 2003, Wiley Series in Probability and Statistics

   Volume  Google Scholar

7. Blom G: Statistical Estimates and Transformed Beta Variables. 1958, New York: John Wiley and Sons, Inc.

   Google Scholar

8. Harter HL: Expected values of normal order statistics. Biometrika. 1961, 48: 151-165. 10.1093/biomet/48.1-2.151.

   Commodity  Google Scholar

9. Cramér H: Mathematical Methods of Statistics. 1999, Princeton University Press

   Google Scholar

10. Bland G: Estimating hateful and standard deviation from the sample size, three quartiles, minimum, and maximum. International Journal of Statistics in Medical Research, in printing. 2014,

    Google Scholar

11. Liu T, Li Thousand, Li 50, Korantzopoulos P: Clan between c-reactive poly peptide and recurrence of atrial fibrillation subsequently successful electrical cardioversion: a meta-assay. J Am Coll Cardiol. 2007, 49: 1642-1648. ten.1016/j.jacc.2006.12.042.

    CAS  Article  PubMed  Google Scholar

12. Zhu A, Ge D, Zhang J, Teng Y, Yuan C, Huang Yard, Adcock IM, Barnes PJ, Yao X: Sputum myeloperoxidase in chronic obstructive pulmonary disease. Eur J Med Res. 2014, 19: 12-10.1186/2047-783X-nineteen-12.

    Commodity  PubMed  PubMed Key  Google Scholar

13. Higgins JPT, Green South: Cochrane Handbook for Systematic Reviews of Interventions. 2008, Wiley Online Library

    Book  Google Scholar

Pre-publication history

• The pre-publication history for this paper tin can be accessed here:http://www.biomedcentral.com/1471-2288/14/135/prepub

Download references

Acknowledgements

The authors would like to thank the editor, the associate editor, and two reviewers for their helpful and effective comments that greatly helped improving the final version of the article. Ten. Wan's research was supported by the Hong Kong RGC grant HKBU12202114 and the Hong Kong Baptist University grant FRG2/13-14/005. T.J. Tong'south research was supported by the Hong Kong RGC grant HKBU202711 and the Hong Kong Baptist Academy grants FRG2/xi-12/110, FRG1/13-14/018, and FRG2/13-xiv/062.

Author information

Author notes

Affiliations

1. Department of Estimator Science, Hong Kong Baptist Academy, Kowloon Tong, Hong Kong

   Xiang Wan & Jiming Liu

2. Department of Statistics, Northwestern University, Evanston, IL, U.s.a.

   Wenqian Wang

3. Department of Mathematics, Hong Kong Baptist University, Kowloon Tong, Hong Kong

   Tiejun Tong

Corresponding author

Correspondence to Tiejun Tong.

Additional information

Competing interests

The authors declare that they have no competing interests.

Authors' contributions

TT, XW, and JL conceived and designed the methods. TT and WW conducted the implementation and experiments. All authors were involved in the manuscript preparation. All authors read and approved the final manuscript.

Xiang Wan, Wenqian Wang contributed equally to this piece of work.

Electronic supplementary material

Authors' original submitted files for images

Rights and permissions

Open Admission This article is licensed under a Creative Commons Attribution 4.0 International License, which permits employ, sharing, adaptation, distribution and reproduction in whatever medium or format, as long as you requite appropriate credit to the original author(s) and the source, provide a link to the Artistic Commons licence, and signal if changes were made.

The images or other third political party material in this commodity are included in the article's Artistic Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article'due south Artistic Commons licence and your intended utilize is not permitted by statutory regulation or exceeds the permitted apply, you volition demand to obtain permission directly from the copyright holder.

To view a re-create of this licence, visit https://creativecommons.org/licenses/past/four.0/.

The Artistic Commons Public Domain Dedication waiver (https://creativecommons.org/publicdomain/goose egg/ane.0/) applies to the data made available in this article, unless otherwise stated in a credit line to the information.

Reprints and Permissions

About this article

Cite this article

Wan, X., Wang, Due west., Liu, J. et al. Estimating the sample hateful and standard divergence from the sample size, median, range and/or interquartile range. BMC Med Res Methodol 14, 135 (2014). https://doi.org/10.1186/1471-2288-14-135

Download citation

• Received: 05 September 2014

• Accustomed: 12 December 2014

• Published: xix December 2014

• DOI : https://doi.org/ten.1186/1471-2288-14-135

Keywords

• Interquartile range
• Median
• Meta-analysis
• Sample hateful
• Sample size
• Standard difference

Source: https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/1471-2288-14-135

Posted by: aguirremardeen1966.blogspot.com

Share this post